Les mathématiques derrière la conception du sextant
Ces principes expliquent la raison de la conception géométrique du sextant, l’utilisation de ses miroirs, ainsi que la raison pour laquelle les graduations du limbe correspondent à l’angle entre l’horizon et l’astre à relever (cf. schéma du sextant sous la démonstration mathématique).
Application des principes mathématiques et géométriques du sextant :
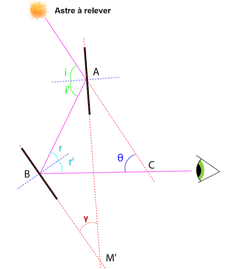
Représentation schématique du sextant avec A le grand miroir, B le petit et C la lunette de visée
Cette formule en apparence complexe décrit en fait simplement le fonctionnement du sextant et l'application des règles de l'optique dictées par les lois de Snell-Descartes : le rayon incident (venant le l'astre) entre en contact avec le grand miroir A avec l'angle i. Ce dernier est réfléchi selon i', de même valeur, sur le petit miroir B avec un angle r. Il est alors réfléchi avec un angle r' de même valeur vers la lunette. Ceci nous permet de déterminer la valeur de l'angle γ, qui vaut i-r. Grâce à la loi des angles alternes internes, on peut voir que γ est aussi l'angle CAM', c'est-à-dire l'angle que fait l'alidade lorsqu'on la déplace. En utilisant ces valeurs, on détermine ensuite la valeur de θ, qui est égal au double de γ, ce qui explique d'ailleurs pourquoi le limbe est gradué en demi-degrés et non en degrés.
Sources :
https://fr.wikipedia.org/wiki/Sextant
Une animation expliquant la géométrie de l'objet : http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/optige...'horizon.
Ce contenu suit le billet : "Le sextant : principe de fonctionnement" et précède "Comment utiliser correctement un sextant ?"

Commentaire(s)
Ajouter un commentaire