Dans le domaine de l’astronomie et de la navigation, le sextant permet de mesurer la hauteur angulaire d’un astre au-dessus de l’horizon, et par la suite, de déterminer à partir de calculs réalisés au préalable, notre position sur le globe, c’est-à-dire notre latitude selon l’équateur et notre longitude selon le méridien de Greenwich. Bien qu’on ne voie pas de prime abord de de lien entre une hauteur et un angle réalisé par un sextant, il faut savoir que les milles marins (unité de mesure utilisée en navigation) lient ces deux grandeurs : 1 mille marin vaut 1 degré d’arc, soit un angle de 1°. Bien que n’étant fait que d’un arc de 60° apparents, le sextant est en fait gradué de demi-degrés, ce qui lui permet de réaliser des mesures du double d’envergure. Ebenezer Hoppe, lui, doit sûrement penser à cette époque que 120° ne sont pas assez, c’est donc pour ceci qu’il décide de modifier un modèle de la manière suivante : rajouter une alidade de verre graduée, elle-même montée au-dessus des graduations du limbe. Ainsi, les demi-degrés sont à nouveau divisés par deux ; on obtient donc des quarts de degré, et les mesures passent d’une portée de 2x60° à 4x60°, c’est-à-dire 240° (parler de demis et quarts de degrés est un abus de langage, on devrait en effet parler de doubles et quadruples degrés). Pour autant, cette théorie ne put s’appliquer en pratique, et les mesures ne purent être augmentées qu’à 140°, ce qui relevait toujours d’une amélioration des systèmes précédents.

Pour fonctionner, un sextant doit vérifier deux principes :

-   Le milieu entourant l’objet doit être transparent, homogène (mêmes propriétés physiques en tout point) et isotrope (en tout point du milieu, ces caractéristiques ne doivent pas changer) : pour résumer, le milieu ambiant ne doit pas dévier les rayons lumineux.

-   Également, le sextant applique les lois de Snell-Descartes, notamment une de la réflexion : les angles incidents et réfléchis sont égaux en valeur absolue , car l’indice de réfraction de l’air est le même en tout point.

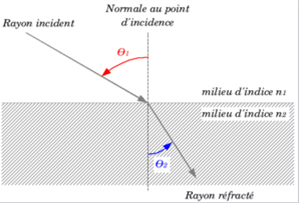
Pour faire simple, le sextant est fait pour fonctionner dans l’air, mais ne pourrait marcher dans l’eau, par exemple.

   Comme nous l'avons vu, le sextant s’avère être un instrument de conception complexe, alors que son but n’est que de mesurer un angle entre l’horizon et un objet dans le ciel. On peut donc se demander la raison derrière la conception géométrique du sextant, et on pourrait se dire qu’un sextant plus simple pourrait être fait d’une lunette teintée que l’on pointerait que l’on pointerait vers un astre, et d’un fil à plomb vertical qui indiquerait un angle augmentant au fur et à mesure que l’on monterait la lunette, pourtant il n’en est rien. 

En rouge l’axe de la lunette, dirigée sur l’astre, en bleu le fil à plomb vertical, en vert l’angle thêta, augmentant plus on lève la lunette haut dans le ciel. 

   En effet, ceci introduirait de nombreux problèmes : comment, en visant librement dans le ciel, sans aucun repère, être garanti de viser le centre de l’astre avec la lunette ? Peut-on être sûr de ne pas être aveuglé si on pointe une lunette, même teintée, vers l’astre ? Comment réaliser une mesure s’il y a du vent qui fait bouger le fil à plomb ? Trop de variables interviennent, et la conception actuelle du sextant les élimine toutes : 

-   Il permet de viser le centre en alignant ce dernier avec l’horizon ce qui est déjà plus précis, et viser quelque chose droit devant nous est plus simple que de viser longtemps quelque chose haut dans le ciel

-   Regarder dans une lunette un rayon émis par un astre est bien moins dangereux que de regarder l’astre en lui-même

-   L’arc de cercle et le limbe en métal, sur des plans parallèles, permettent de ne pas se faire de souci en cas de vent

Sources : 

https://books.google.fr/books?id=LNgVDAAAQBAJ&pg=PA180&lpg=PA180&dq=hopp...'s%20improved%20sextant&f=false

https://fr.wikipedia.org/wiki/Sextant

navastro.free.fr

Ce billet suit le diaporama "Le premier GPS ?" et précède le billet "les mathématiques derrière la conception du sextant"

-